WAT Note(III).
Top > Blog Posts > (本記事)

このブログにKaTeXを導入してみた

Tatsuroh Wakasugi
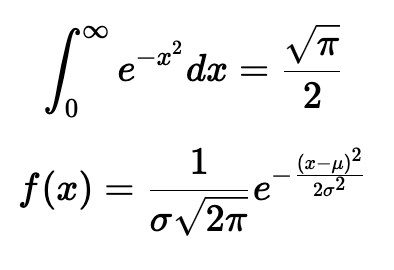
Tatsuroh Wakasugi

たまに学生時代にやってた数学をもう一度学び直したいと思う時があり、このブログにも復習記事を書いてみたらどうか？と思ったが、その際に数式がうまく記事上で表記できない問題に出くわしていた。

数式を綺麗に表示できるものと言えばよく学生時代のレポートで使った TeX が思い浮かぶだろう。私も懐かしいものである。

このブログのような Web 上でも TeX のような表記ができるものがあったりしないだろうか？と思って調べたところKaTeXなるものがあるらしいと聞いたので、それを使ってみる事にした。

KaTeX とは

KaTeX は、Khan Academy によって開発された、Web 上で数式を美しく高速に表示するための JavaScript ベースのライブラリである。以下の特徴がある。

  • 高速なレンダリング
  • ブラウザ非依存の一貫した表示
  • TeX や LaTeX の構文をサポート
  • 軽量（約 200KB）
  • クライアントサイド・サーバーサイド両方での利用が可能

導入・利用方法

KaTeX を導入する方法は以下の２つがある。

1. CDN を使用する方法

HTML ファイルの head セクションに以下のコードを追加すれば OK 。（比較的簡単で推奨されている）

<!DOCTYPE html>
<!-- KaTeX requires the use of the HTML5 doctype. Without it, KaTeX may not render properly -->
<html>
  <head>
    <!-- ここから -->
    <link
      rel="stylesheet"
      href="https://cdn.jsdelivr.net/npm/katex@0.16.21/dist/katex.min.css"
      integrity="sha384-zh0CIslj+VczCZtlzBcjt5ppRcsAmDnRem7ESsYwWwg3m/OaJ2l4x7YBZl9Kxxib"
      crossorigin="anonymous"
    />
    <script
      defer
      src="https://cdn.jsdelivr.net/npm/katex@0.16.21/dist/katex.min.js"
      integrity="sha384-Rma6DA2IPUwhNxmrB/7S3Tno0YY7sFu9WSYMCuulLhIqYSGZ2gKCJWIqhBWqMQfh"
      crossorigin="anonymous"
    ></script>
    <script
      defer
      src="https://cdn.jsdelivr.net/npm/katex@0.16.21/dist/contrib/auto-render.min.js"
      integrity="sha384-hCXGrW6PitJEwbkoStFjeJxv+fSOOQKOPbJxSfM6G5sWZjAyWhXiTIIAmQqnlLlh"
      crossorigin="anonymous"
      onload="renderMathInElement(document.body);"
    ></script>
    <!-- ここまで -->
  </head>
  ...
</html>

※KaTeX のバージョンが時期により異なる場合があるので、公式ページ1にある表記も参考のこと。

auto-render.min.js も指定することで、HTML 内でオートレンダリングが可能になります。

そして、HTML 内で以下のように使用する。

<div>\[ \int_0^\infty e^{-x^2}dx = \frac{\sqrt{\pi}}{2} \]</div>

<!-- または -->
<div>$$ \int_0^\infty e^{-x^2}dx = \frac{\sqrt{\pi}}{2} $$</div>

2. npm を使用する方法

プロジェクトで npm を使用している場合

npm install katex

で katex のモジュールをインポートできる。

そして、JavaScript ファイルで以下のように使用する。

import katex from "katex";
import "katex/dist/katex.min.css";

// 数式のレンダリング
katex.render("c = \\pm\\sqrt{a^2 + b^2}", element, {
  throwOnError: false,
});

実用例

このブログにも KaTeX を導入してみたので、いくつか表記をしてみる。実際の例を確認したい。（うまく変換されてない場合は連絡ください。。）

例えば

1. 二次方程式の解の公式

x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

（表記例）

x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}

2. オイラーの公式

e^{ix} = \cos x + i\sin x

（表記例）

eix=cos⁡x+isin⁡xe^{ix} = \cos x + i\sin x

3. ガウス分布

f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}

（表記例）

f(x)=1σ2πe−(x−μ)22σ2f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}

今後数学系の記事を出すことがあるかはまだ未定だが、ある場合は活用したい。

Footnotes

  1. KaTeX(公式ページ) ↩